在几何学中,直线与平面平行的判定定理是研究平行关系的重要工具之一。通过该定理,我们可以判断给定的直线是否与平面平行,从而帮助我们解决一些几何问题。本文将介绍直线与平面平行的判定定理及其应用。
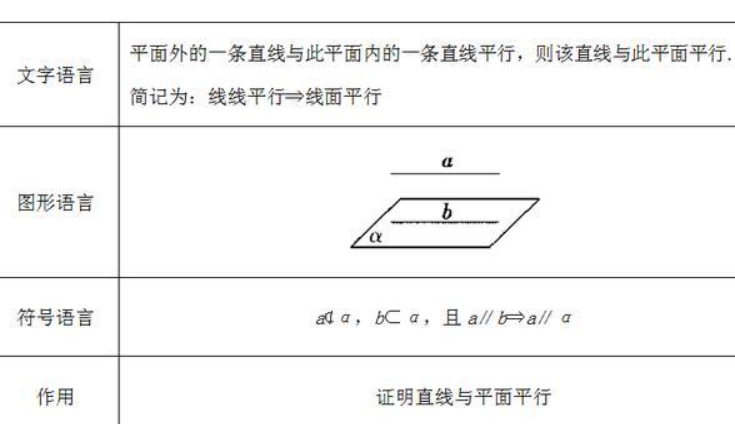
一、直线与平面平行的判定定理
直线与平面平行的判定定理是基于平行关系的定义而推导出来的结论。要判断一条直线与一个平面是否平行,可以通过以下两种方法进行考察:
1.1 直线与平面的法向量关系
设直线L的一个方向向量为a,平面P的法向量为n,若a与n垂直,则直线L与平面P平行。
1.2 直线上的任意两点的向量关系
设直线L上的两个点A、B,平面P的任意一点为C。若向量AB与向量AC平行,则直线L与平面P平行。

二、直线与平面平行的应用
直线与平面平行的判定定理在几何学中具有广泛的应用。下面我们将介绍其中的两个应用场景:
2.1 平行线判定
根据直线与平面平行的判定定理,我们可以判断两条直线是否平行。假设有两条直线L1和L2,通过判断它们与同一个平面P的平行关系,可以得出它们是否平行。如果直线L1与平面P平行,并且直线L2也与平面P平行,那么直线L1与L2就是平行的。
2.2 直线与平面的垂直关系
直线与平面平行的判定定理还可以用于判定直线与平面的垂直关系。根据定理的定义,如果直线L的方向向量与平面P的法向量垂直,则可以得出直线L与平面P垂直。这一性质在计算机图形学中有着重要的应用,可以帮助我们计算直线与平面的交点,进而实现线段与平面的交互效果。
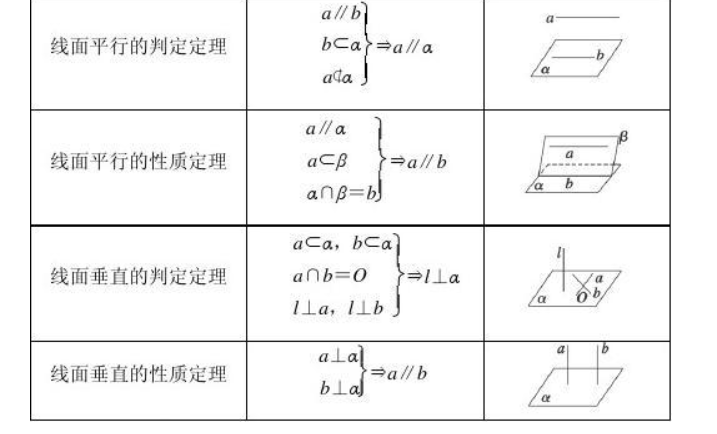
结语:
直线与平面平行判定定理是几何学中重要的推理工具。通过该定理,我们可以判断直线与平面之间的关系,进而解决一些几何问题。同时,了解该定理的应用场景,可以更好地应用于实际问题的解决中。希望通过本文的介绍,读者能对直线与平面平行判定定理有更深入的理解。