线面平行是几何学中一个重要的概念,也是许多问题的基础。证明线面平行的方法有很多种,本文将从多个方面对这些方法进行详细的阐述,以帮助读者更好地理解这个概念。
1、平行线的定义和性质
平行线是指在同一个平面内,永远不相交的两条直线。证明线面平行的方法之一就是通过平行线的定义和性质来进行推导。在这个方面,我们可以从以下几个方面进行阐述:
(1)平行线的定义
(2)平行线的性质
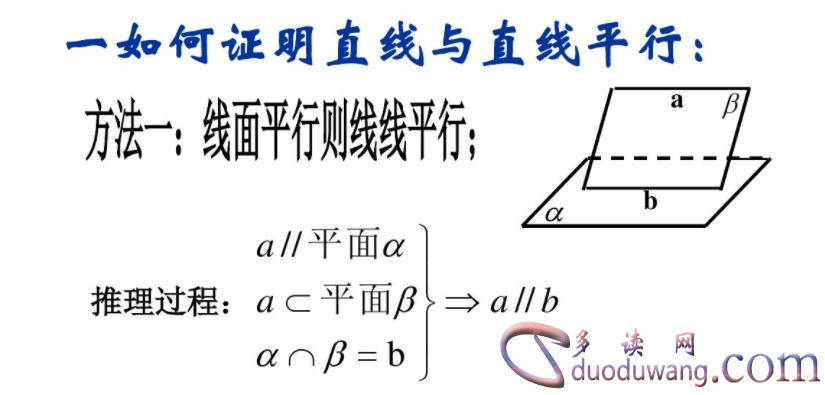
(3)利用平行线的性质证明线面平行
2、角度的性质
角度是几何学中一个基本的概念,也是证明线面平行的重要方法之一。在这个方面,我们可以从以下几个方面进行阐述:
(1)角度的定义和性质
(2)利用角度的性质证明线面平行
(3)角度的度量
3、相似三角形的性质
相似三角形是指两个三角形的对应角度相等,对应边成比例。在证明线面平行的过程中,相似三角形也是一种重要的方法。在这个方面,我们可以从以下几个方面进行阐述:
(1)相似三角形的定义和性质
(2)利用相似三角形的性质证明线面平行
(3)相似三角形的判定方法
4、向量的性质
向量是几何学中一个重要的概念,也是证明线面平行的一种方法。在这个方面,我们可以从以下几个方面进行阐述:
(1)向量的定义和性质
(2)利用向量的性质证明线面平行
(3)向量的加减法
5、平面的性质
平面是几何学中一个基本的概念,也是证明线面平行的重要方法之一。在这个方面,我们可以从以下几个方面进行阐述:
(1)平面的定义和性质
(2)利用平面的性质证明线面平行
(3)平面的投影
6、交错线的性质
交错线是指两条交错的直线,它们的内错角和外错角互为补角。在证明线面平行的过程中,交错线也是一种重要的方法。在这个方面,我们可以从以下几个方面进行阐述:
(1)交错线的定义和性质
(2)利用交错线的性质证明线面平行
(3)交错线的判定方法
7、平行四边形的性质
平行四边形是指两组平行的对边相等的四边形。在证明线面平行的过程中,平行四边形也是一种重要的方法。在这个方面,我们可以从以下几个方面进行阐述:
(1)平行四边形的定义和性质
(2)利用平行四边形的性质证明线面平行
(3)平行四边形的判定方法
8、
通过以上的阐述,我们可以看出证明线面平行的方法是多种多样的,每种方法都有其独特的优势和适用范围。在实际应用中,我们需要根据具体的问题来选择合适的方法。无论采用哪种方法,我们都需要对其进行深入的研究和理解,以便更好地应用到实际问题中。