直线与平面垂直的性质定理是几何学中非常重要的一个定理。它是建立在欧氏几何公理的基础上的,是几何学的基础之一。我们将从多个方面对这个定理进行详细的阐述,希望能够帮助读者更好地理解这个定理。
1、直线与平面垂直的定义
直线与平面垂直的定义是:如果直线上的任意一点到平面的距离都相等,那么这条直线与平面垂直。这个定义是直观的,也是我们理解直线与平面垂直的基础。
2、直线与平面垂直的性质
直线与平面垂直的性质有很多,其中比较重要的有以下几个:
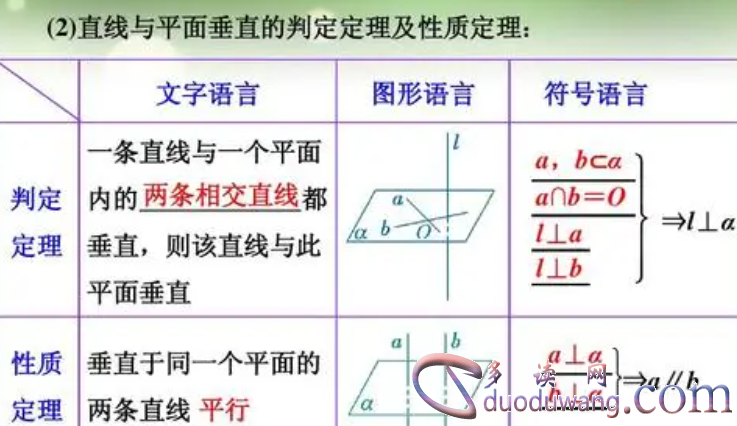
① 直线与平面垂直的两个条件
直线与平面垂直的两个条件是:直线在平面内,且直线与平面的任意一条交线都与平面垂直。这个条件是判断直线与平面垂直的基本条件。
② 直线与平面垂直的性质
直线与平面垂直的性质有很多,其中比较重要的有以下几个:
1) 直线与平面垂直的两个向量的点积为0。
2) 直线与平面垂直的两个向量的叉积为平面的法向量。
3) 直线与平面垂直的两个向量分别在直线和平面的法向量上投影的乘积为0。
这些性质可以帮助我们更深入地理解直线与平面垂直的本质。
3、直线与平面垂直的应用
直线与平面垂直的应用非常广泛,其中比较重要的有以下几个:
① 直线与平面垂直的应用于计算平面的法向量
我们可以通过直线与平面垂直的性质,计算出平面的法向量。这对于计算机图形学、计算机视觉等领域非常有用。
② 直线与平面垂直的应用于求解问题
在几何学中,我们经常会遇到一些问题,需要求解直线与平面垂直的情况。这时,我们可以利用直线与平面垂直的定义和性质,来求解问题。
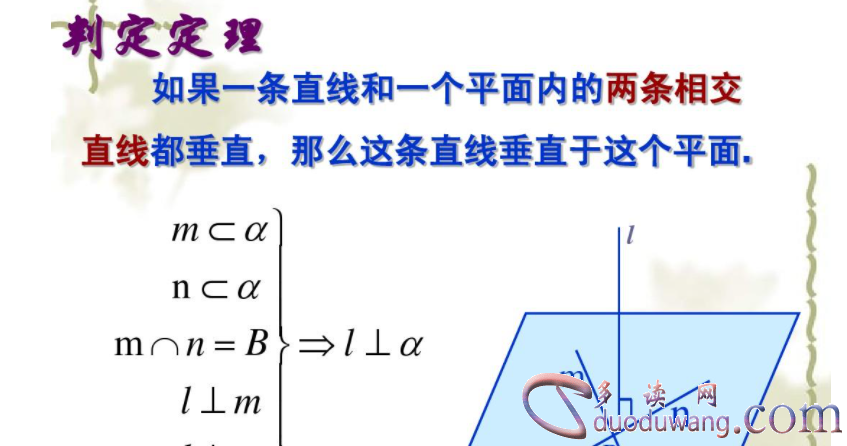
4、直线与平面垂直的证明
直线与平面垂直的证明是几何学中比较复杂的证明之一。我们可以通过欧氏几何公理,来证明直线与平面垂直的定理。这个证明过程比较复杂,需要一定的几何学知识和技巧。
直线与平面垂直的性质定理是几何学中非常重要的定理,它是几何学的基础之一。我们从定义、性质、应用和证明等多个方面对这个定理进行了详细的阐述。希望能够帮助读者更好地理解这个定理,并在实际应用中得到运用。