在几何学中,直角三角形全等指的是两个直角三角形的对应边相等,对应角相等。那么我们如何判断两个直角三角形是否全等呢?下面将介绍直角三角形全等的判定方法。
1. 直角三角形全等的条件是什么?
直角三角形全等的条件是:两个直角三角形的一个直角和一个锐角相等,且所夹的一边相等。也就是说,两个直角三角形的一条边与对边的夹角相等,且对应的两边分别相等。

2. 判断两个直角三角形是否全等的步骤?
画出两个直角三角形的示意图,确保对应的边和角要对应相等。
根据两个直角三角形的角和边的对应关系,分别定义为∠A、∠B、∠C、∠D为直角三角形ABC和DEF的对应角。
再次,分别定义AB、BC、AD、DC分别为直角三角形ABC和DEF的对应边。
最后,根据已知条件,利用对应角和对应边的关系,判断两个直角三角形是否全等。
3. 直角三角形全等的判定方法
直角三角形全等有两种判定方法,分别为SSA(一个锐角和两边相等)、SAS(两边和所夹的角相等)。
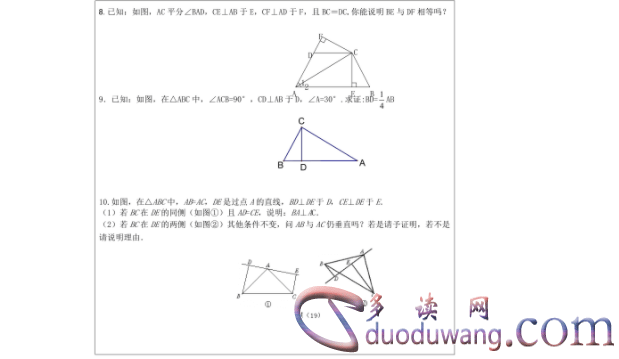
- SSA判定方法
当两个直角三角形的一个直角和两个对应边相等时,即直角三角形ABC和DEF中∠A=∠D,AB=DE,AC=DF,则直角三角形ABC≌DEF。
- SAS判定方法
当两个直角三角形的两个边和夹角相等时,即直角三角形ABC和DEF中AB=DE,∠A=∠D,AC=DF,则直角三角形ABC≌DEF。
4. 例题演练
例如,已知直角三角形ABC中∠A=90°,AB=5,AC=12;直角三角形DEF中∠D=90°,DE=5,DF=12,求证明ABC≌DEF。根据已知条件可得,∠A=∠D=90°,AB=DE=5,AC=DF=12。因此,根据SAS判定方法,可得直角三角形ABC≌DEF。
通过以上介绍,我们了解了直角三角形全等的判定方法。在判定两个直角三角形是否全等时,需要注意对应角和对应边的关系,并根据SSA和SAS判定方法进行分析。直角三角形全等的判定方法能够帮助我们快速准确地判断两个直角三角形是否全等,为几何学习提供了重要的辅助。