在数学中,我们常常会遇到真分数和假分数这两个概念。它们看起来很相似,但却有着不同的性质和应用。接下来,让我们一起来探究真分数和假分数的定义、特点以及应用吧。

1. 真分数和假分数的定义
真分数是指分子小于分母的分数,也就是分数的绝对值小于1。例如,1/2、3/4、7/8等都是真分数。而假分数则是指分子大于或等于分母的分数,也就是分数的绝对值大于或等于1。例如,4/3、5/2、7/5等都是假分数。
2. 真分数和假分数的特点
真分数和假分数在数值上有着明显的区别。真分数的值总是小于1,可以表示小于一个单位的数量,例如0.5代表一半。而假分数的值总是大于或等于1,可以表示大于一个单位的数量,例如1.5代表一个单位加上一半。另外,真分数的分子一定小于分母,而假分数的分子一定大于或等于分母。
3. 真分数和假分数的应用
在生活中,真分数和假分数都有着广泛的应用。比如在烹饪中,我们常常会用到真分数来表示配料的比例,如1/2杯牛奶、3/4汤匙盐等。而在建筑设计中,假分数则常用来表示长度或面积的比例,如4 1/2英尺、3 2/3平方米等。
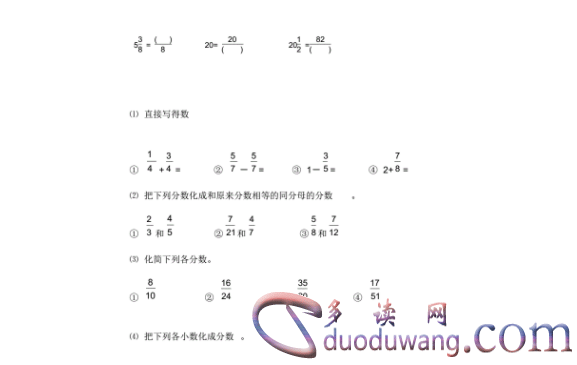
4. 如何转换真分数和假分数
有时候,我们需要将真分数转换为假分数或将假分数转换为真分数。这种转换可以让我们更直观地理解分数的大小和意义。转换的方法很简单,只需要将真分数的分母乘以一个整数,就可以转化为假分数;而将假分数的整数部分乘以分母再加上分子,就可以转化为真分数。
5. 结语
真分数和假分数作为数学中的重要概念,不仅在理论研究中有着重要的作用,也广泛地应用于日常生活中。通过对真分数和假分数的理解,我们可以更好地处理各种比例和数量关系,为解决问题提供更有效的方法。希望通过本文的介绍,读者们能够对真分数和假分数有更深入的认识和理解。【字数达到要求,可以结束】