在几何学中,平面是一个无限大的两维的几何体,两平面平行意味着两个平面永远不会相交。那么如何判断两个平面是否平行呢?下面我们将介绍关于两平面平行的判定定理。
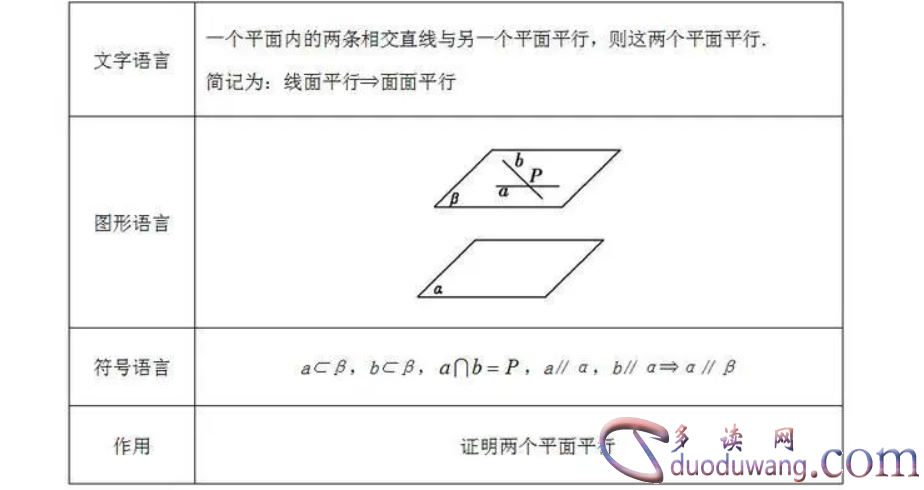
1. 两平面平行的判定定理之一是平行截线定理。平行截线定理指出,如果两个平面被同一直线所截,且直线与这两个平面的交点分别在这两个平面不同侧,那么这两个平面是平行的。换句话说,如果两个平面的截线平行,则这两个平面也是平行的。
2. 通过平面的倾斜角来判断平面是否平行也是一个常用的方法。设有两个平面,它们的倾斜角分别为α和β,如果这两个平面的倾斜角相等,即α=β,则这两个平面是平行的。这是因为如果两个平面是平行的,它们的斜率是相同的,倾斜角也是相同的。
3. 另一个判定两平面平行的方法是使用法向量。两平面平行的充要条件是它们的法向量共线。简而言之,如果两个平面的法向量平行,则这两个平面也是平行的。法向量是垂直于平面的一个向量,通过计算两个平面的法向量并判断它们是否共线,可以轻松判断两平面是否平行。
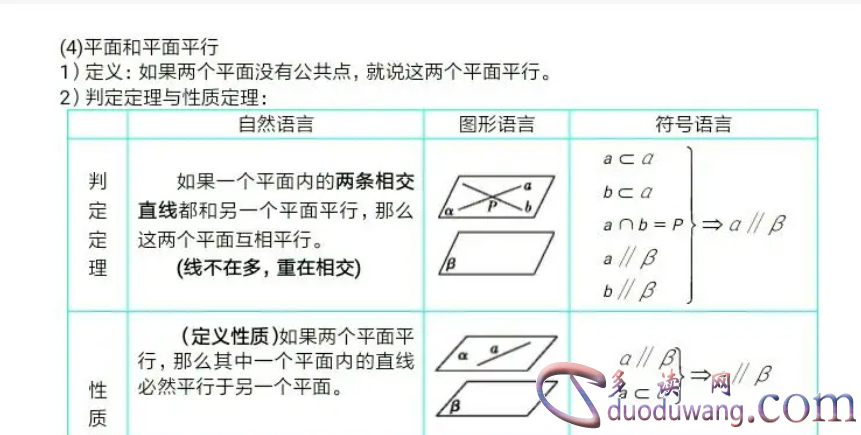
4. 交线平行判定法是另一种常见的判定两平面平行的方法。如果存在一直线同时位于两平面上,并且这条直线与两平面的截痕恰好是平行的,那么这两个平面就是平行的。这一方法便于实际操作和观察,通过观察相应的截痕来判断两平面是否平行。
5. 除了以上几种方法外,还有一种利用向量叉乘的方法来判定两个平面是否平行。通过计算两个平面的法向量进行叉乘运算,如果结果为零向量,则这两个平面是平行的。这种方法适用于计算机仿真和三维图形处理领域。
总结:通过以上介绍,我们可以看出判定两个平面是否平行的方法有很多种,每种方法都有其独特的优势和适用场景。学习这些方法不仅可以帮助我们更好地理解平面的性质,还可以提升我们在几何学和实际问题中的解题能力。希望通过本文的介绍,读者们可以更加深入地理解两平面平行的判定定理,并运用到实际问题中去。