三角函数是数学中重要的一个分支,其有许多重要的性质和公式。本文将为大家介绍三角函数中的一种经典公式——诱导公式。
1. 什么是三角函数的诱导公式?
三角函数的诱导公式是指将一个三角函数的关系式通过某些运算,转化为另一个三角函数的关系式。常见的诱导公式有和差化积、倍角公式、平方公式等。通过这些公式,我们可以简化复杂的三角函数表达式,便于计算和研究。
2. 和差化积的诱导公式
和差化积是三角函数中的常见运算方法,通过将两角的和或差的三角函数关系转化为同一个三角函数的关系,方便计算。例如,sin(a+b) = sinacosb + cosasinb, cos(a-b) = cosacosb + sinasinb。
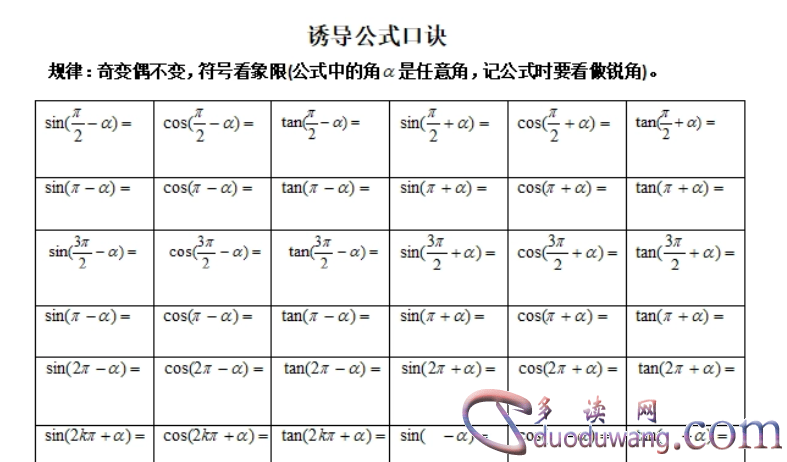
3. 倍角公式的诱导公式
倍角公式是常用的三角函数诱导公式,可以将一个角的两倍或半角的三角函数关系转化为原三角函数的关系。例如,sin2a = 2sinacos, cos2a = 1-2sin^2a。
4. 平方公式的诱导公式
平方公式也是三角函数中的重要公式,可将三角函数的平方关系转化为和差关系,方便计算。例如,sin^2a = 1/2(1-cos2a), cos^2a = 1/2(1+cos2a)。
5. 为什么三角函数的诱导公式重要?
三角函数的诱导公式在数学研究和应用中起到重要的作用。通过这些公式,我们可以简化繁杂的三角函数表达式,快速计算各种三角函数的值,解决实际问题和推导重要结论。诱导公式还能扩展三角函数的应用领域,拓宽数学研究的范围。

6. 如何灵活应用三角函数的诱导公式?
灵活应用三角函数的诱导公式需要熟练掌握各种公式和运算技巧,理解其推导原理和作用特点。在实际问题中,可以根据具体问题的特点到合适的诱导公式,简化计算过程,提高解题效率。同时,多练习题目,加深对三角函数的理解和应用能力。
7. 结语
三角函数的诱导公式是数学中的重要工具,通过合理运用这些公式,可以简化复杂问题的处理,加深对三角函数的理解,提高数学研究和实际问题解决的效率。希望大家能够认真学习和掌握三角函数的诱导公式,发挥其潜在的作用,拓展数学应用领域,做到知行合一,为数学研究和应用做出贡献。