全等三角形是几何学中的基本概念,在我们的日常生活中也随处可见。全等三角形指的是两个三角形的所有对应边相等,所有对应角相等,它们的形状完全一样,只是位置或大小不同。在判定两个三角形是否全等时,我们有几种方法可以使用。
要判断两个三角形是否全等,必须要满足以下条件:(1) 两个三角形的三边对应边相等;(2) 两个三角形的三个内角分别相等。只有同时满足这两个条件,我们才能够确定两个三角形是全等的。
接着,我们可以使用SSS(三边边长相等)判定法来判断两个三角形是否全等。当两个三角形的三条边两两对应相等时,我们可以通过SSS定理来判断它们是全等的。例如,若三角形ABC和三角形DEF的AB=DE,BC=EF,AC=DF,那么我们可以得出结论,这两个三角形是全等的。

然后,我们可以使用SAS(一边和与其两个内角之和相等)判定法来判断两个三角形是否全等。当两个三角形的一个边和其两个内角之和分别相等时,我们可以通过SAS定理来判断它们是全等的。例如,若三角形ABC和三角形DEF的AB=DE,∠A=∠D,∠B=∠E,那么我们可以得出结论,这两个三角形是全等的。
最后,我们可以使用ASA(两边和夹角之和相等)判定法来判断两个三角形是否全等。当两个三角形的两个角和夹在它们之间的边分别相等时,我们可以通过ASA定理来判断它们是全等的。例如,若三角形ABC和三角形DEF的∠A=∠D,∠B=∠E,AC=DF,那么我们可以得出结论,这两个三角形是全等的。
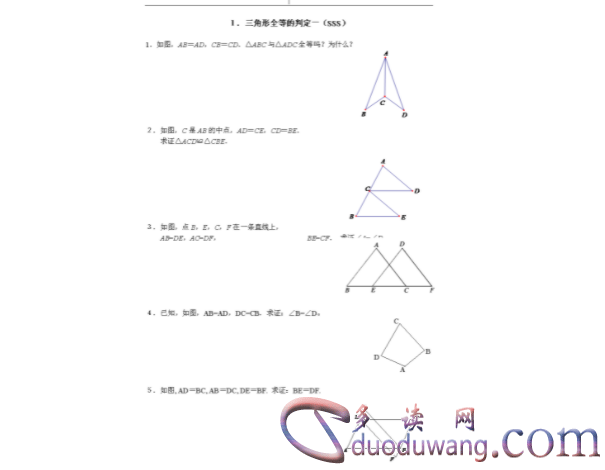
总结:判断两个三角形是否全等,我们可以使用SSS、SAS、ASA这三种方法。在实际运用中,我们根据已知条件来到合适的方法进行判断。对于学生来说,掌握全等三角形的判定方法是十分重要的,因为全等三角形的性质不仅在几何学中有广泛的应用,也在日常生活中有诸多实际意义。希望通过本文的介绍,能够帮助大家更好地理解和掌握全等三角形的判定方法,提高几何学习的效率和成绩。