平面几何是数学中的一个重要分支,平面与平面垂直的性质定理是平面几何中的一个基础概念。在平面几何中,两个平面相互垂直是指它们的法线互相垂直,即两平面法线的夹角为90度。下面我们来详细介绍一些和平面垂直相关的性质定理。
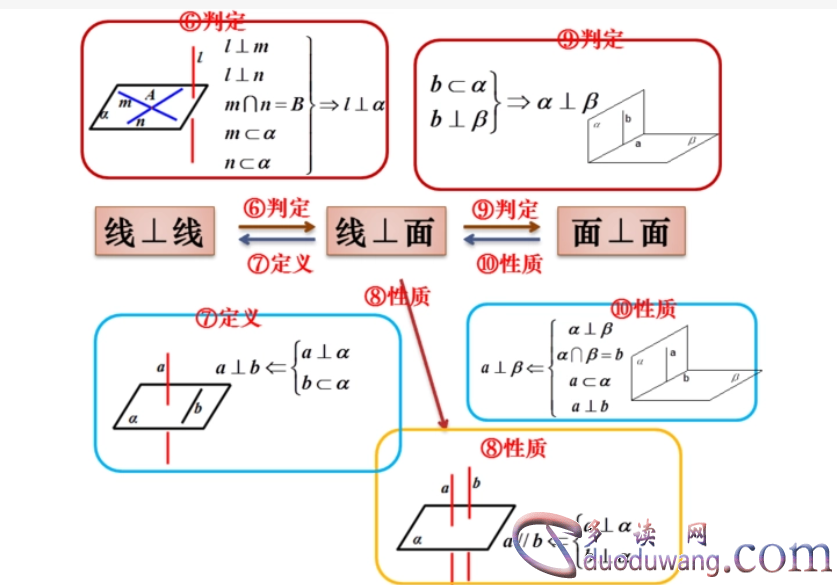
1. 两个平面相交于一条直线,且一平面的法线与另一平面的法线垂直。
在平面几何中,如果两个平面相交于一条直线,那么这两个平面就是相互垂直的。这是因为相交形成的直线也是两平面的交线,而两平面的交线和两平面的法线互相垂直,所以这两个平面是相互垂直的。
2. 一个平面与另一个平面的垂直平分直线的夹角。
如果一个平面与另一个平面垂直,那么这两个平面的交线就是直线,这条直线被称为它们的平分线。也就是说,这条直线将这两个平面的夹角等分,使得夹角的两个部分相等。
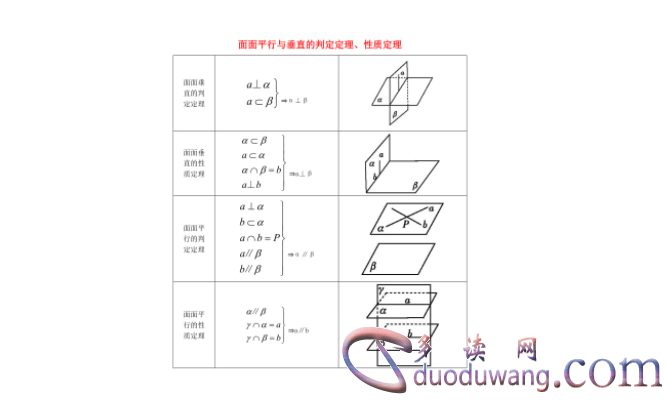
3. 两个平行平面与同一平面垂直的直线,这两个平面平行。
在平面几何中,如果一个平面与另一个平面垂直于同一直线,而这两个平面之间还是平行的,那么这两个平面就是平行的。这是因为垂直于同一直线的两个平面之间的夹角是90度,而平行的两个平面之间的夹角也是90度,所以这两个平面是平行的。
4. 一个平面与平面外的一条直线垂直,那么这条直线与平面的交点到平面的距离是相等的。
在平面几何中,如果一个平面与一条直线垂直,那么这条直线与平面的交点到平面的距离是相等的。这是直线与平面的性质决定的,也是平面几何中的一个重要概念。
总结:平面与平面垂直的性质定理在平面几何中有着重要的地位,它们是平面几何中的基础概念,对于理解平面几何的性质和规律非常重要。希望以上的介绍能够帮助读者理解并掌握这些重要的性质定理。