弦切角定理是几何学中的重要定理之一,它描述了圆上某条弦所成的角与该弦两边的角度关系。通过证明弦切角定理,我们可以更深入地了解圆的性质和应用。下面我们来详细探讨一下这一定理的证明过程。
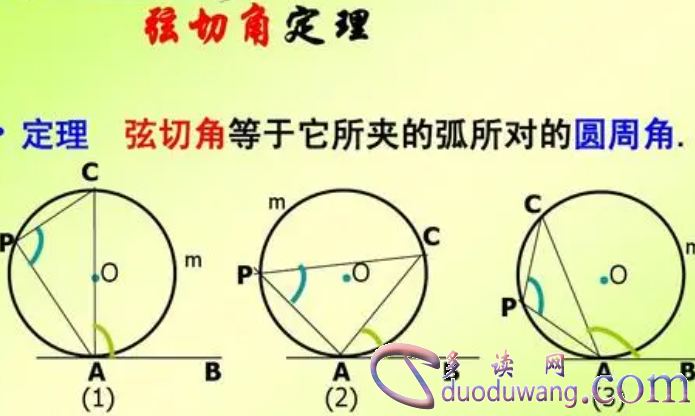
1. 画出圆和弦
我们在纸上画一个圆,并且画一条直线作为该圆的弦。这条弦将圆分成两个部分,我们将这两个部分分别标记为A和B。
2. 连接切点和圆心
接着,在圆上画一条线作为切线,该切线与弦相切于弦的中点,然后我们将切点、圆心和弦的中点连接起来,形成一个三角形。
3. 观察角度关系
观察这个三角形的角度关系,我们会发现切线与弦的交点处的角为直角。同时,弦与切点连接的线段与切点与圆心连接的线段平行。这时我们可以设定一些符号,比如设切点、圆心和弦的中点的连线为线段b,这样我们可以表示出各个角度和线段之间的关系。

4. 利用几何定理
根据几何定理,我们知道平行线与交线夹出的角相等,所以我们可以得出几个角相等的等式。根据三角形内角和定理,我们可以得到三角形内所有角的和为180度。
5. 推导弦切角定理
通过不断推导和运用几何定理,我们最终可以证明出弦切角定理:「圆中一条弦上的切线,斜率等于与该弦在圆中央相对的两条弦的角的一半」。
6. 应用弦切角定理
弦切角定理在几何学中有广泛的应用,它不仅可以帮助我们计算各种几何图形中的角度关系,还可以应用到实际生活中的种种问题中。比如在建筑学中,我们可以利用弦切角定理来计算建筑物中各个角度的大小,确保建筑的结构稳固和外观优美。
通过本文的分析和证明过程,我们更加深入地理解了弦切角定理的本质和应用。通过不断研究几何学中的定理和原理,我们可以提高自己的逻辑思维能力和数学素养。弦切角定理虽然看似简单,却蕴含着丰富的数学奥秘,它是我们探索几何世界的重要工具之一。愿我们在学习和探索中不断进步,发现更多数学之美。