在数学中,log是一种常见的运算符号,它表示对数运算。log的运算法则是数学中的基本规则之一,它可以简化复杂的对数计算,并提供了一种便捷的方法来解决一系列与对数相关的问题。下面将介绍log的运算法则,帮助读者深入理解和应用这一重要的运算法则。

一、指数和对数的关系
在log的运算法则中,指数和对数是密切相关的。指数是对数运算的反向操作,可以通过对数运算来求解。具体而言,如果m = log(base a)n,则n = a^m。这个关系对于计算和验证指数和对数具有重要的意义。
二、对数的换底公式
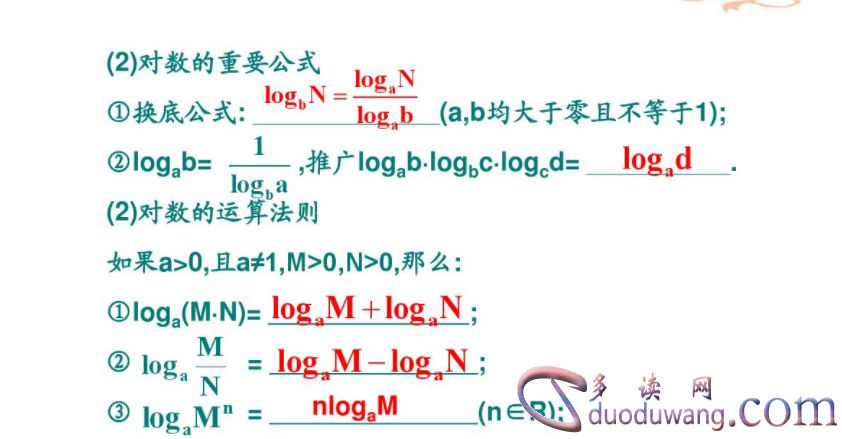
换底公式是log运算中的一条重要法则,它可以用来将一种底数的对数转换为另一种底数的对数。具体而言,如果m = log(base a)n,则m = log(base b)n / log(base b)a,其中a、b、n为正实数且a≠1,b≠1。换底公式的应用可以简化对数计算,将计算问题转化为已知底数的对数运算。
三、对数的乘法法则
对数的乘法法则是log运算中的一条重要规则,它可以用来简化对数中的乘法运算。具体而言,log(base a)(m*n) = log(base a)m + log(base a)n。根据这个法则,我们可以将一个对数的乘法运算转化为多个对数的加法运算,从而提高计算效率。

四、对数的除法法则
对数的除法法则是log运算中的一条常用法则,它可以用来简化对数中的除法运算。具体而言,log(base a)(m/n) = log(base a)m - log(base a)n。根据这个法则,我们可以将一个对数的除法运算转化为多个对数的减法运算,简化了计算过程。
五、对数的幂法法则
对数的幂法法则是log运算中的一条重要法则,它可以用来简化对数中的幂运算。具体而言,log(base a)(m^p) = p * log(base a)m。根据这个法则,我们可以将一个对数的幂运算转化为对数与常数的乘法运算,方便进行计算。
六、对数的指数法则
对数的指数法则是log运算的基本法则之一,它可以用来计算指数运算中的对数。具体而言,log(base a)(a^m) = m。根据这个法则,我们可以计算出底数为a的指数运算中的对数。
总结:
log的运算法则是数学中的重要工具,它可以简化复杂的对数计算,提供了一种便捷的方法来解决与对数相关的问题。在实际应用中,我们可以根据对数的运算法则,将一个复杂的对数运算转化为已知底数的简单运算,从而节省时间和精力。因此,深入理解和熟练应用log的运算法则对于数学学习和实际问题的解决具有重要的意义。通过不断练习和应用,我们可以更好地掌握log的运算法则,提高自己的数学能力。