三角函数是数学中重要的一部分,它们在解决几何问题、物理问题以及工程问题时起着重要的作用。而三角函数的诱导公式是指通过已知的三角函数公式推导出其他三角函数公式的一种方法。本文将介绍三角函数公式诱导公式的原理以及几个常用的诱导公式。
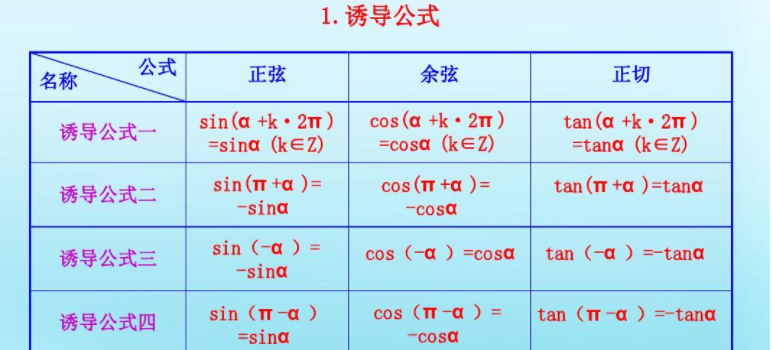
1. 三角函数公式的基本原理
三角函数公式包括正弦函数、余弦函数、正切函数等。这些函数之间存在一系列的关系,可以通过诱导公式相互推导。例如,我们知道正弦函数的定义是以直角三角形中的一条边与斜边的比值而得到的,而余弦函数则是以另外一条边与斜边的比值得到的。
2. 正弦函数和余弦函数的诱导公式
正弦函数和余弦函数的诱导公式是最常用的。以正弦函数的诱导公式为例,我们可以通过余弦函数的定义和三角恒等式得到:
sin(A+B) = sinA * cosB + cosA * sinB
同理,利用三角恒等式可以推导出余弦函数的诱导公式如下:
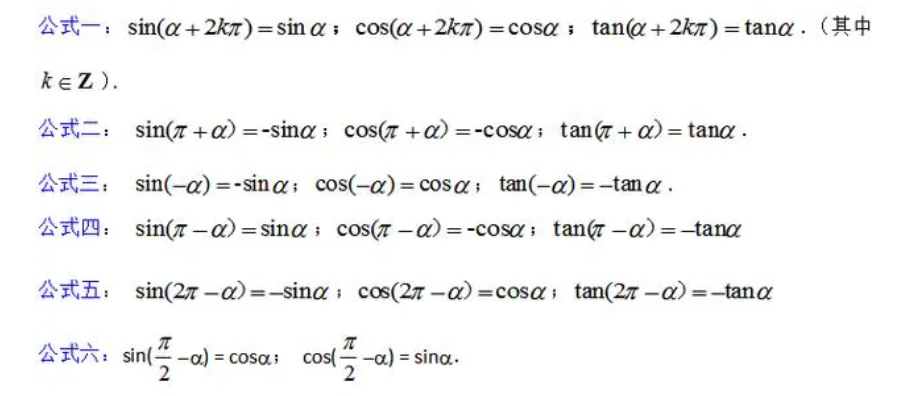
cos(A+B) = cosA * cosB - sinA * sinB
3. 正切函数的诱导公式
正切函数的诱导公式可以通过正弦函数和余弦函数的诱导公式推导得到。我们可以将正切函数表示为 sinA/cosA。然后,利用三角恒等式可以得到:
tan(A+B) = (sinA * cosB + cosA * sinB) / (cosA * cosB - sinA * sinB)
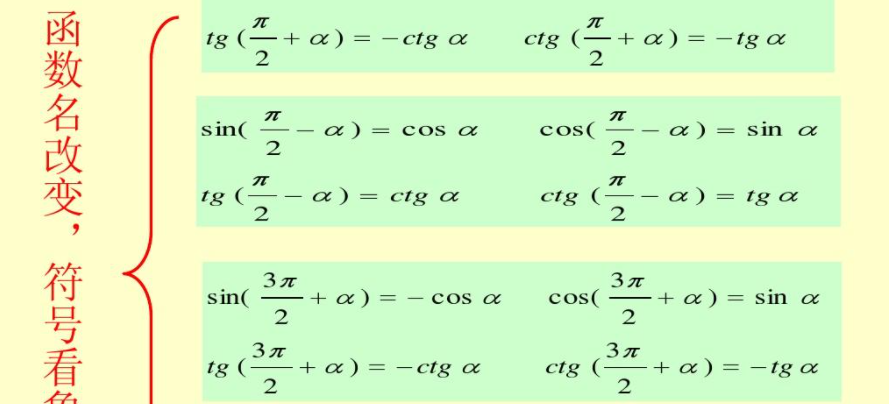
4. 通过诱导公式解决实际问题
利用三角函数的诱导公式,我们可以在解决实际问题时更便利地进行计算。例如,在测量塔高时,我们可以通过测量角度和距离,利用诱导公式计算出塔的高度。又如,在物理实验中,通过测量物体的斜坡上的角度和长度,通过诱导公式,我们可以计算出物体的加速度等重要参数。
结语:
三角函数诱导公式是解决三角函数问题的重要工具,通过掌握诱导公式可以更高效地解决实际问题。本文介绍了三角函数公式诱导公式的原理以及常用的诱导公式,希望读者能够通过学习掌握三角函数诱导公式,提高解决实际问题的能力。