三角函数是数学中非常重要的概念之一,常用于解决各种几何问题和物理问题。其中,诱导公式是三角函数中的重要内容之一,它可以帮助我们通过一个角的三角函数值来找到其他的角的三角函数值。在本文中,我们将介绍常见的三角函数诱导公式以及它们的推导过程。
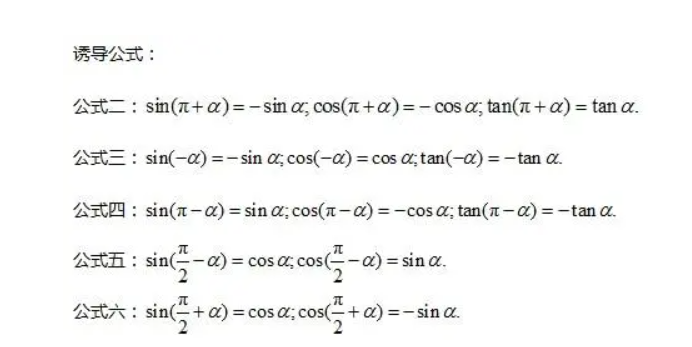
一、正弦函数的诱导公式:
我们知道,正弦函数是一个周期为2π的函数,在每一个周期内它的取值范围是[-1,1]。现在,我们来推导正弦函数的诱导公式。
假设角A的正弦值为sin(A),那么它对应的弧度为A,在单位圆上的坐标为(x,y)。根据单位圆的性质,我们可以得到以下关系:
x = cos(A)
y = sin(A)
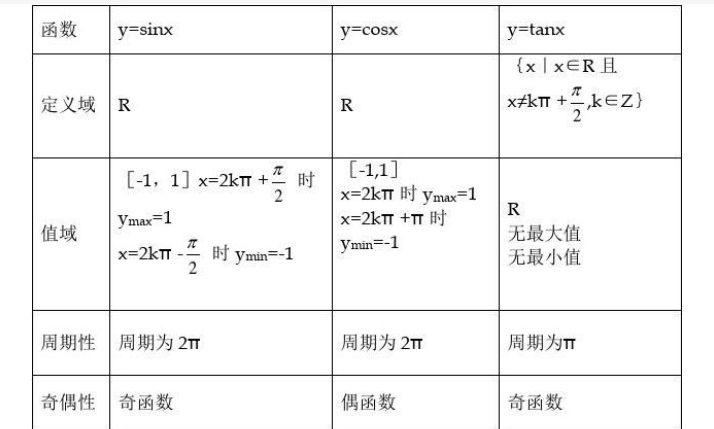
二、余弦函数的诱导公式:
余弦函数也是一个周期为2π的函数,在每一个周期内它的取值范围也是[-1,1]。现在,我们来推导余弦函数的诱导公式。
假设角A的余弦值为cos(A),那么它对应的弧度为A,在单位圆上的坐标为(x,y)。根据单位圆的性质,我们可以得到以下关系:
x = cos(A)
y = sin(A)
三、正切函数的诱导公式:
正切函数是一个在每个周期内都无界的函数,它的取值范围是整个实数集。现在,我们来推导正切函数的诱导公式。
假设角A的正切值为tan(A),那么它对应的弧度为A,在单位圆上的坐标为(x,y)。根据单位圆的性质,我们可以得到以下关系:
x = cos(A)
y = sin(A)
四、余切函数的诱导公式:
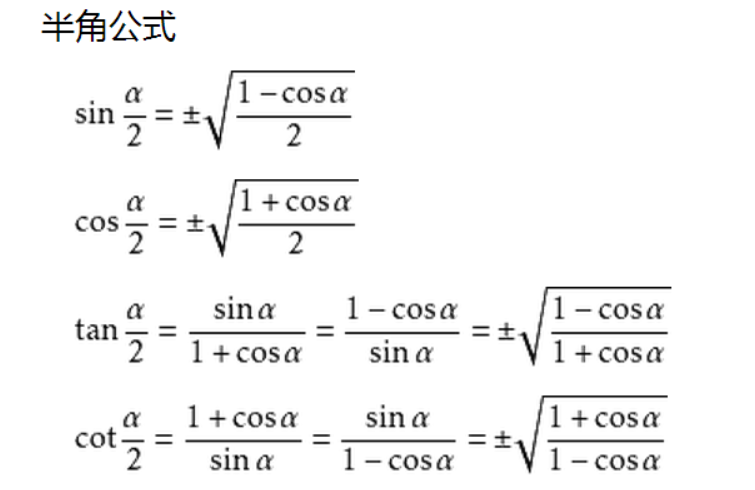
余切函数也是一个在每个周期内都无界的函数,它的取值范围是整个实数集。现在,我们来推导余切函数的诱导公式。
假设角A的余切值为cot(A),那么它对应的弧度为A,在单位圆上的坐标为(x,y)。根据单位圆的性质,我们可以得到以下关系:
x = cos(A)
y = sin(A)
五、正割函数和余割函数的诱导公式:
正割函数和余割函数也是常见的三角函数,它们分别是余弦函数的倒数和正弦函数的倒数。它们的诱导公式可以通过正弦函数和余弦函数的诱导公式推导得到,具体的过程略。
结语:
三角函数的诱导公式是数学中的重要内容,它可以帮助我们通过一个角的三角函数值找到其他的角的三角函数值。在本文中,我们介绍了正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数的诱导公式,并给出了它们的推导过程。掌握了这些诱导公式,我们就可以更加方便地解决各种与三角函数相关的问题。